Hogyan találjuk meg az egyszerű háromdimenziós alakok felületét

Tartalom

• irányok
• Kockák, prizmák és gömbök
• Hengerek és kúpok
• Amire szüksége van

Hogyan találjuk meg az egyszerű háromdimenziós alakok felületét. Adjon mélyebbet a világ területére.

irányok

Kockák, prizmák és gömbök

1. Keresse meg a kocka felületét úgy, hogy az egyik oldalon a hosszúság négyzetét megtalálja, és megszorozza az eredményt 6. Példa: A 3 oldal kocka felülete 6 x (3 x 3) = 54.

2. Számítsa ki a területet mindkét oldalon, és adjon hozzá mindet, hogy megtalálja a prizma területét. Példa: A téglalap alakú prizma 2-es magasságának, a 3-as szélességnek és az 5-ös hosszúságnak a kiszámításához (2 x 3) + (2 x 3) + (2 x 5) + (2 x 5) + (3 x 5) + (3 x 5) = 62.

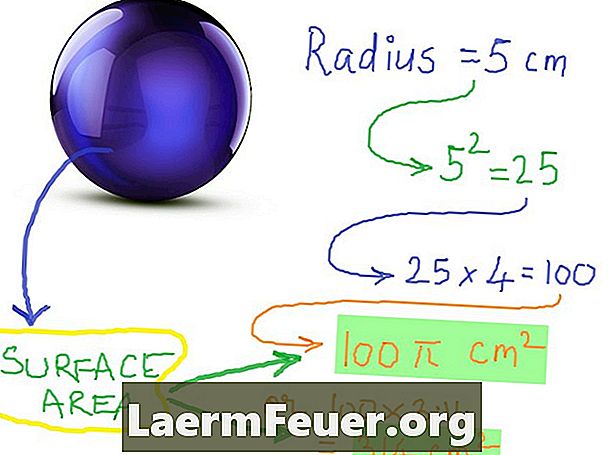
3. A gömbterület megkereséséhez szorozza meg a négyzet sugarát pi-vel. Ezután megszorozzuk az eredményt 4-gyel. Példa: A 3-as sugarú gömb felülete 4 x pi x 3 x 3 = 113.

   
   

Hengerek és kúpok

1. Először keressük meg a henger felületét a rádiusz szorzásával 2-szeresével.

2. Szorozzuk meg a terméket hengermagassággal.

3. Szorozzuk a sugár négyzetét 2-szeresével.

4. Keresse meg az 5. és 6. lépésben kapott eredmények összegét. Példa: A 4-es és 5-ös sugarú henger felülete (2 x pi x 4 x 5) + (2 x pi x 4 x 4) = 226.

5. Határozzuk meg a kúp felületét úgy, hogy az alap sugarát megszorozzuk a kúp dőlésszögének magasságával.

6. Szorozzuk az eredményt pi-vel.

7. Szorozzuk a bázis sugara négyzetét pi-vel

8. Keresse meg a 9. és 10. lépések eredményének összegét. Példa: A kúp felületének a 2 bázis sugara és a 4 lejtő magassága a (pi x 2 x 4) + (pi x 2 x 2) = 38.

   
   

Amire szüksége van

• Rajzkönyvek
• számológépek
• Iránytű rajzolása
• gumik
• mappák
• Diagrampapírok
• notebook
• uralkodók