Tartalom
- Határozza meg a levegőben töltött időt.
- 1. lépés
- 2. lépés
- 3. lépés
- 4. lépés
- Határozza meg a maximális magasságot
- 1. lépés
- 2. lépés
- 3. lépés
- Határozza meg a megtett vízszintes távolságot.
- 1. lépés
- 2. lépés
- 3. lépés
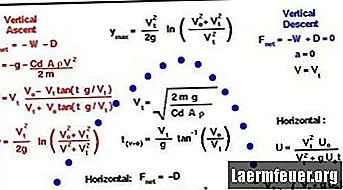
Itt van a módszer a golyó pályájának kiszámításához, és különösen a levegőben töltött idő, a pálya tartománya és legmagasabb pontja. Ebben a példában néhány feltételezést tettek a számítás egyszerűsítésére: elhanyagolható a légellenállás, nincs szél és nincs elég lőtávolság a Föld forgásának életbe lépéséhez.
Határozza meg a levegőben töltött időt.
1. lépés
Először meg kell határozni az íj alakját. Ha a szög kezdetben lefelé irányul, akkor már ismert, hogy a legmagasabb pont a lőállás. Még egy felfelé irányuló szög is a cél lehet a legmagasabb pont, függetlenül attól, hogy ez a szög sekély vagy megfelelő magasságú (h). Ezt a negyedik lépésben lehet meghatározni, amikor meghatározzuk a levegő idejét.
2. lépés
Ha a szög "?" a lövés sebessége a lövedék kezdeti pályája és a vízszintes között, tehát a kezdeti függőleges sebesség V (i) = V.sen?
3. lépés
A levegőidőt a h = V.sen? .T - (0.5) g.t ^ 2 helyzet egyenletével állapíthatjuk meg, ahol g = 9,8 méter / másodperc ^ 2. Minden változó ismert, a levegőben töltött idő kivételével, t, így ez a másodfokú függvény segítségével megoldható: ax ^ 2 + bx + c = 0, ezért x = [-b ± √ (b ^ 2-4ac )] / 2a
4. lépés
Ha egynél több megoldás megengedett a t számára, mivel h> 0, akkor az első eredmény megegyezik azzal, amikor a magasság = h a mászási úton, a második pedig akkor, amikor a magasság = h az ereszkedési úton. Ha h <0, akkor az egyetlen valódi megoldás t-re megengedett, a másik pedig negatív.
Határozza meg a maximális magasságot
1. lépés
Ha? <0, akkor már ismert, hogy a maximális magasság a kezdeti magasság, h = 0.
2. lépés
Ha egynél több idő volt, t, amelyben a golyó h-ra nyúlik, akkor a legkisebb t egy repülési útnak felel meg, ahol h a legmagasabb pont. A legnagyobb t megfelel annak a golyónak, amely magasabb magasságot ér el, mielőtt visszatérne a h-hoz. Ennek a magasságnak a megoldására a V (t) = V (0) - 9,8t képletet használják t értékének megtalálásához, amikor a függőleges sebesség nulla. Más szavakkal: t, V.sen? = 9,8 t?
3. lépés
A t megoldása és a magassági képlet összekapcsolása megadja a maximális magasságot: hm = V.sen? - 4,9t ^ 2. Ugyanezt a megközelítést alkalmazzák a maximális magasságú megoldásnál is, ha csak egy t-re vonatkozó megoldást engedélyeztek.
Határozza meg a megtett vízszintes távolságot.
1. lépés
Ahhoz, hogy meghatározza a megtett vízszintes távolságot, mire a golyó eléri a h magasságot, először számítsa ki a golyó kezdeti vízszintes sebességét: v (i) = V.cos (?).
2. lépés
Helyezze be a t időt, amikor a golyó eléri az A végső magasságot, a képlet helyzetében vízszintes sebességgel: A = V.cosΘ.t. Feltéve, hogy a jobb oldalon nincs légellenállás és nincs gyorsulási kifejezés.
3. lépés
Ha egynél több idő volt t, amikor a magasság h-ban volt, akkor az "A" két pozíció érvényes lesz, és az elért legmagasabb pont hm lesz a két "A" közül a kisebbnél. A vízszintes és függőleges végállások, valamint az elért legmagasabb pont már ismertek, ezáltal meghatározva a golyó pályáját.